Геометрия — просто!

Добрый день, друзья!
Мы продолжаем решение задач из сборника «ОГЭ-2015 математика».
И сегодня у нас на очереди задания 09 — геометрия углы и стороны треугольника.
Это первое задание по геометрии, которое включает в себя достаточно простые упражнения.
Тем не менее, для их решения необходимо знать теорию
7-8 классов — равнобедренный треугольник и его свойства;
сумма внутренних углов треугольника и 6 свойств из этого правила; прямоугольный треугольник и его свойства;|
теорема Пифагора; формулы площади треугольника.
А теперь приступим к заданиям.
То, что мы не проговорили по теории, пройдём в процессе решения.

Задание 1. На стороне АВ треугольника АВС  выбрана точка D таким образом, что AD=AC.
Угол А треугольника равен 10º,
а угол АСВ равен 166º.
Необходимо найти угол DCB.
Решение: Если в треугольнике две стороны равны,
то это треугольник — равнобедренный.
А в равнобедренном треугольнике углы при основании равны.
Т.е.  ADC=ACD.
Вместе с тем, сумма углов треугольника равна 180º. 
Поэтому, сумма углов А, ADC и ACD равна 180º.
Но угол А равен 10º.
Значит на долю двух равных углов  ADC и ACD приходится 180-10=170º.
Поэтому, каждый угол равен 170:2 = 85º.
Итак, угол ACD равен 85º, а по условию, угол АСВ равен 166º.
Значит, угол DCB равен 166º-85º= 81º.
Ответ: угол DCB равен 81º.

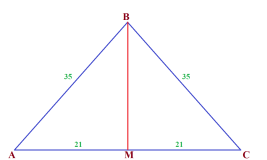Задание 2. Дан треугольник АВС. Две стороны его АВ и ВС равны 35.
Третья сторона АС равна 42.
Необходимо найти
длину медианы ВМ.
Решение: Как и в первой задаче — две стороны треугольника равны.
А это значит, что
треугольник — равнобедренный.
А медиана угла при вершине  равнобедренного  треугольника является одновременно биссектрисой и высотой.
Значит, ВМ перпендикулярно АС. Т.е. угол АМВ — прямой.
Треугольник АВМ — прямоугольный.
Поскольку медиана делит противоположную сторону
треугольника пополам, то АМ=42:2 = 21.
АВ равно 35 по условию.
Из прямоугольного треугольника, в котором известна
гипотенуза и один из катетов, надо найти второй катет.
ВМ² = АВ² — АМ² = 35² — 21².
Пока остановимся и увидим, что последнее выражение есть
разность квадратов двух чисел.
Она раскладывается на  произведение двух множителей —
сумму этих чисел и их разность. Имеем:
35² — 21² = (35-21)(35+21) = 14•56 = 2•7•7•8 = 16•49
Теперь из этого выражения необходимо извлечь корень, чтобы найти ВМ.
ВМ = √(16•49) = 4•7 = 28.
Ответ: длина медианы ВМ равна 28.

Задание 3. Площадь прямоугольного треугольника равна 128√3. Один из острых углов равен 30º.
Найти длину катета, лежащего напротив этого угла.
Решение: площадь прямоугольного треугольника равна половине произведения его катетов.
Примем катет, лежащий против угла в 30º за х. А второй катет за у.
Тогда тангенс  угла в 30º из треугольника равен отношению х/у.
С другой стороны табличное значение тангенса 30º равно √3/3.
Отсюда х/у = √3/3
Получим 3х = √3у  или у = х√3
Переходим к площади треугольника:
S = 1/2  ху = 1/2  х•х√3 = 128√3
х²√3/2 = 128√3
х² = 256
х=16
Ответ: катет, лежащий против угла в 30º, равен 16.

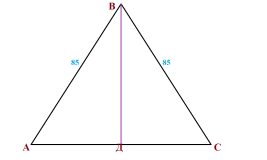Задание 4. Периметр равнобедренного треугольника равен 250,
а боковая сторона — 85.
Найти площадь треугольника.
Решение: периметр — это сумма трёх сторон треугольника.
Сумма двух боковых сторон равна 85+85 = 170.
Значит, основание равно
220-170 = 80.
Медиана, она же высота, проведённая из вершины угла равнобедренного треугольника,
делит основание пополам.
Половина основания равна 80:2 = 40.
Из прямоугольного треугольника ВСД по
теореме Пифагора найдем высоту треугольника.
ВД² = ВС² — ДС² = 85² — 40² = (85-40)(85+40) = 125•45 = 25•5•5•9
ВД = 5•5•3 = 75.
Отсюда, площадь треугольника равна
половине произведения основания на высоту.
S = 1/2  • 80 • 75 = 75 • 40 = 3000
Ответ: площадь треугольника равна 3000.

Задание 5.  В треугольнике АВС
ВМ — медиана,  ВН — высота.
Дано АС = 348, НС = 87, ∠АСВ = 17º. Необходимо найти  угол АМВ.
Решение: Поскольку ВМ — медиана, то АМ=МС = 348/2 = 174.
Нам дано, что НС = 87.
Значит, МН = 174 — 87 = 87.
Получается, что высота ВН делит сторону МС в треугольнике МВС пополам, а это значит, что
высота является медианой.
Такое может быть только в равнобедренном треугольнике.
Получается, что ВМ=ВС. И ∠АСВ=∠ВМС = 17.
Но угол АМВ смежный с углом ВМС.
А смежные углы в сумме дают 180º.
Отсюда, угол АМВ равен 180 — 17 = 163.
Ответ: угол АМВ равен 163º.

На сегодня всё.
Успехов и до новых задач!
С 1 сентября всех, с Днём Знаний!