Геометрия — просто!

Друзья, добрый день!
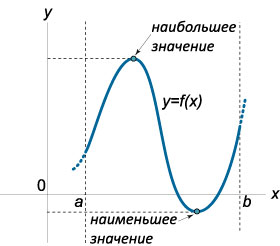
Сегодня мы начнём разбирать 12 задание ЕГЭ,
в котором необходимо найти
наименьшее значение функции,
точку минимума или максимума функции с помощью производных.
Задание достаточно простое,
если знать
формулы производных,
уметь решать
простейшие квадратные уравнения
и отыскивать
интервалы знакопостоянства.
Давайте приступим.

Задание 1. Найти наименьшее значение функции  у = √(х²  + 10х + 106)
Решение: покажем два решения данного задания.
А. Берём производную по у и приравниваем её к нулю.
В тех точках, в которых производная равна нулю, функция имеет либо максимум, либо минимум.
Данная функция сложная. Поэтому берём производную от сложной функции:
у´ = (2х + 10)/2√(х²  + 10х + 106) = 0
Дробь равна нулю  в том случае, когда числитель её равен нулю, а знаменатель существует.
Выражение, стоящее под знаком корня всегда положительное, т.к. дискриминант его — отрицательный.
Приравниваем числитель дроби к нулю: 2
х + 10 = 0 х + 5 = 0 х = — 5
Имеем одну точку на числовой прямой.
Правее этой точки знак производной всегда положительный.
Левее этой точки знак меняется на противоположный, т.е. на минус.
При переходе производной с минуса на плюс через ноль, у функции в этой точке — минимум.
Подставляем -5 в значение  у = √(х²  + 10х + 106)
у(-5) = у = √(25  — 50 + 106) = √81 = 9
Б. Возводим в квадрат правую и левую части уравнения у = √(х²  + 10х + 106)
у² = х²  + 10х + 106
Теперь берём производную от правой и левой части
2у´ = 2х + 10
у´ = х + 5
у´ = 0 при х = -5.
Далее как  в решении А.
Ответ: наименьшее значение функции 9.

Задание 2. Найти наибольшее значение функции у = √(-х²  + 6х + 40)
Решение: Ещё один вариант решения данного задания.
Под корнем стоит выражение -х²  + 6х + 40, которое в силу ООФ должно быть не менее нуля.
Графически — это парабола и ветви её направлены вниз.
Найдем точки пересечения этой параболы с осью ОХ.
-х²  + 6х + 40 = 0
х²  — 6х — 40 = 0   Решая это уравнение по теореме Виета находим корни
х1 = 10   х2 = -4
Максимальное значение функции находится в вершине параболы.
Абсцисса вершины находится между корнями, т.е. в точке х = 3.
Находим у(3) = √(-9   + 6·3 + 40) = √49 = 7.
Решая это задание через производную, получим:
у² = -х²  + 6х + 40
2у´ = -2х + 6
у´ = -х + 3
у´ = 0 при х = 3.
Далее получаем максимум функции равен  7.
Ответ: 7.

Задание 3. Найти точку минимума функции   у = (х + 24)е^{х – 70}
Решение: производная произведения равна производной первого множителя, умноженной на второй множитель плюс производной второго множителя, умноженной на первый множитель.
Ещё надо учесть, что второй множитель — сложная функция.
у´ = (х + 24)´е^{х – 70}  + (х + 24)(е^{х – 70} )´ = 0
у´ = е^{х – 70}  + (х + 24)е^{х – 70}  = 0
е^{х – 70} (1 + х + 24) = 0
Произведение двух множителей равно нулю в том случае, если один из них равен нулю.
Показательная функция нулю никогда не равна, значит нулем может быть выражение в скобке.
х + 25 = 0
х = — 25.
Ответ: точка минимума функции — 25.

Задание 4. Найдите наименьшее значение функции у = (х – 23)²е^{2х – 44}      на отрезке [1;23].
Решение: Задание похоже на задание № 3 с той лишь разницей, что первый множитель здесь тоже является сложной функцией.
 у´ = [(х – 23)²]´е^{2х – 44}   +  (х – 23)² (е^{2х – 44})´ = 0
2(х — 23) е^{2х – 44} + (х – 23)² (е^{2х – 44})·2 = 0
2(х — 23)е^{2х – 44} (1 + х — 23) = 0
х — 23 = 0        х = 23
х — 23 + 1= 0   х = 22
Производная имеет два корня, т.е. равна нулю в двух точках.
А это значит, что в точках
х = 22 и х = 23 функция имеет максимум или минимум.
Чтобы определить в какой точке максимум, а в какой минимум, строим числовую прямую.

______+_____22______-_____23______+____

 Правее правого корня производная всегда положительна.
При переходе через корень она меняет знак на противоположный.
В точке х = 22 производная меняет знак с плюса на минус — значит у функции в этой точке — максимум.
В точке х = 23 производная меняет знак с минуса на плюс — значит у функции в этой точке — минимум.
Точка х = 23 входит в заданный интервал.
Отсюда у(23) = (23 — 23)е^{2*23 – 44}  = 0
Ответ: наименьшее значение функции 0.

Задание 5. Найдите точку минимума функции   у = 2х^3/2/3 – 5х + 24
Решение: Производная первого одночлена — это производная степенной функции с коэффициентом 2/3.
у´= 3/2 * 2/3 * х½ — 5 = 0
√х — 5 = 0
√х = 5
х = 25.
Ответ: точка минимума функции х = 25.

На сегодня всё.
Успехов все и до новых задач!