 Добрый день!
Добрый день!
Пару дней назад одна из моих читательниц прислала задачу с пометкой — помогите решить задачу по геометрии.
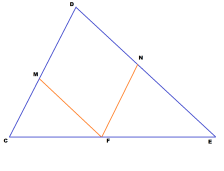
Периметр треугольника CDE равен 55см. в этот треугольник вписан ромб DMFN так, что вершины M, F, и N лежат соответственно на сторонах CD, CE ,и DE. Найдите стороны CD и DE, если CF=8см, EF=12см.
Решение задачи таково:
DNFM — ромб по условию, следовательно MD и FN, а также DN и MF параллельны, как противоположные стороны параллелограмма.
Применим теорему о пропорциональных отрезках, которая говорит, что если на одной стороне угла отложить отрезки, и через их концы провести параллельные прямые, то на другой стороне угла отложатся пропорциональные отрезки.
Т.е., рассматривая угол DEC, CF:FE=DN:NE.
Иными словами, если принять DN за Х,
то NE будет во столько раз больше, чем Х,
во сколько раз FE больше CF. 12:8 = 3/2.
Значит NE = 3Х/2.
Но в ромбе все стороны равны, поэтому, DM=DN=X.
Рассматривая угол DCE, можно сказать,
что DM во столько раз больше СМ, во сколько раз 12 больше 8.
Иными словами СМ= 2Х/3.
Теперь, зная длины всех сторон, пишем уравнение.
Периметр треугольника равен:
2Х/3 + Х + Х + 3Х/2 + 12 + 8 = 55. Или 25Х/6 = 35
Отсюда Х=8,4
3Х/2 = 12,6, следовательно
DE равна 8,4+12,6 = 21
2Х/3 = 5,6,
отсюда CD равно 5,6+8,4 = 14.
Длины сторон 14 и 21.
Успехов!
Вам так же будет интересно:
 Помогите решить задачу по геометрии.
Помогите решить задачу по геометрии.
 Добрый день!
Добрый день!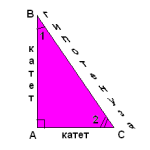


Круг , построенный на большей основе трапеции как на диаметре , касаясь меньшего основания , пересекает боковые стороны и делит их пополам. Найдите меньшую основу трапеции , если радиус окружности равен R.
Если мы соединим точки пересечения боковых сторон трапеции и круга, то получится средняя линия трапеции. Центр круга лежит на середине нижнего основания. Соединяем точки средней линии и центр окружности. Это будут диаметры. Из центра окружности проведём высоту трапеции. Она же будет радиусом круга. Этот радиус перпендикулярен основаниям трапеции и её средней линии. И средняя линия делит его пополам. Получаем прямоугольный треугольник с гипотенузой R и катетом R/2. Найдём второй катет по теореме Пифагора. Он равен R√3/2. Вся средняя линия равна R√3. Отсюда находим верхнее основание трапеции. (X+2R)/2 = R√3. X+2R = 2R√3.
Отсюда верхнее основание равно 2R√3 — 2R или 2R(√3 — 1).
В треугольнике одна точка удалена от сторон на 2:4 и 12 см, а вторая на 4:5 и 9 см соответственно в том же порядке. Найти радиус окружности, вписанной в треугольник.
Добрый вечер, Тамара!
Каждый раз убеждаюсь в том, что геометрия — наука, которая всецело полагается на чертежи. Если мы сделаем чертёж по данным задачи, то получим 3 точки. Причём, третья — это центр вписанной окружности. Перпендикуляры, проведенные к сторонам треугольника, параллельны между собой. А значит все три точки лежат на одной прямой. Так как, являясь секущей, она образует равные соответственные углы. Теперь мы можем построить две прямоугольные трапеции у которых боковые стороны равны между собой. Первая с основаниями 2 и r и между ними 4. Вторая — основания 4 и r и между ними 5. Опустив перпендикуляры на основание трапеций получим два прямоугольных треугольника. Внутри каждого из этих треугольников есть подобные им. И согласно условию подобия мы составляем пропорции:
(r-2)/2 = (r-4)/1
r — 2 = 2r — 8
r = 6.
Получим, что радиус вписанной окружности равен 6 см.
Добрый вечер, помогите решить:
Обьем цилиндра с высотой 10см, равне 250п(см^2).Определить радиус основания конуса с высотой 10см, имеющей такой же обьем как и цилиндр. Определить площадь полной поверхности конуса.
Стас, добрый вечер!
Объём конуса вычисляется по формуле V= 1/3 SH.
Если объём равен 250п, а высота конуса 10, то 250п = 1/3 S*10?
или S = 75п, или R^2 = 75. R = 5 корней из 3.
Площадь полной поверхности конуса из меряется как площадь основания плюс площадь боковой поверхности.
Площадь основания равна 75п.
Площадь боковой поверхности равна произведению половины длины окружности на образующую.
В нашем случае образующую находим из прямоугольного треугольника с катетами 10 (высота конуса) и 5 корней из 3 (радиус окружности).
Она равна корень из 100 + 75 = корень из 175. Или 5 корней из 7.
Подставляем в формулу и считаем:
S бок. = пRl = п* (5 корней из 3)*(5 корней из 7) = 25п корней из 21.
Общая площадь поверхности равна 25п корней из 21 + 75п = 25п(корень из 21 +3).
Успехов!
Здравствуйте помогите пожалуйста решить 2 задачи по геометрии
1 в трапеции ABCD основание AD больше основания BC на 6 см, а средняя линия равна 7 см. Найдите длину отрезков , на которые диагональ АС делит среднюю линию
2 в треугольнике АВС сторону АВ разделяют на 3 равные части и через точки деления проведены прямые, параллельные стороне АС Найти длины отрезков этих прямых, расположеных между сторонами АВ и ВС треугольника, если АС равно 9 см
Никита, добрый вечер!
Если мы построим трапецию и примем верхнее основание за Х, то нижнее основание будет Х+6.
Средняя линия равна полу-сумме оснований.
Составляем уравнение: (Х + Х + 6):2 = 7
Или 2Х + 6 = 14
2Х = 8
Х = 4
Верхнее основание равно 4, нижнее на 6 больше, т.е. 10.
Теперь проведём диагональ АС и среднюю линию МК.
Точку пересечения этих отрезков назовем О.
А теперь рассмотрим треугольник АВС.
МК — средняя линия трапеции, значит, МО — средняя линия треугольника АВС.
А средняя линия равна половине основания.
Отсюда МО равно 1/2 ВС = 1/2*4 = 2.
Второй отрезок равен 5.
Итак, АС делит среднюю линию на отрезки 2 и 5 см.
Во второй задаче работает подобие треугольников.
Пусть точки М и К делят сторону АВ на 3 равные части.
Тогда, АВ относится к КВ как АС относится к верхнему отрезку.
АВ больше КВ в 3 раза, значит, верхний отрезок в 3 раза меньше основания, т.е. равен 3.
МВ меньше АВ в полтора раза, значит, нижний отрезок тоже меньше 9 в полтора раза,
или равен 9:1,5 = 6.
Получаем, отрезки равны 3 и 6 см.
Знайдіть внутрішні кути трикутника,якщо один з них у 3 рази більший за другий.А зовнішній кут при третій вершині дорівнює 100 градусів.
Даша, добрый вечер!
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Значит на 2 угла приходится 100 градусов.
Но один больше другого в 3 раза.
Если примем один угол за Х, тогда второй угол будет 3Х.
В сумме это будет равно х+3Х=4Х.
4Х=100
х=25.
Первый угол равен 25 градусов, второй 3*25 = 75 градусов.
Успехов!
Добрый вечер! Помогите решить Проведите прямую и отметьте на ней точки ABCDK ТАК 1) Точка С принадлежала отрезку с концами в точках А и В 2) точка D принадлежала лучу АВ и не принадлежала отрезку АВ 3)точка К принадлежала лучу ВА и не принадлежала отрезку АВ. Заранее СПАСИБО!
Марина, добрый день!
Точка С лежит внутри отрезка АВ.
Дочка D лежит правее точки В, а точка К лежит левее точки А.
Успехов в освоении геометрии!
Пожалуйста помогите ещё одну задачку . В некотором городе три попарно пересекающиеся улицы. На каждом перекрёстке установлен светофор. Сколько всего светофоров в городе? Было решено проложить новую улицу, пересекающую все старые и не проходящую через уже имеющиеся перекрёстки. Сколько придётся установить светофоров? А если прокладка улиц будет проложена таким же образом, можно ли сказать, сколько будет светофоров в городе с десятью улицами? Спасибо!
Три попарно пересекающиеся улицы образуют треугольник.
Значит, светофоров должно быть три.
Если провести линию, которая пересекает стороны треугольника или их продолжение, то получатся три новые точки.
Т.е. надо ставить три светофора.
Пожалуйсто помогите расписать задачку используя переменные. Найти углы равнобокой трапеции если боковая сторона равна 6 см и разность ее оснований равна 6 см
Здравствуйте, Катя!
Если мы проведем вершин равнобедренной трапеции две высоты, то справа и слева образуются равные прямоугольные треугольники. Нижнее основание каждого треугольника равно полу-разности оснований трапеции, или 3 см.
Боковая сторона трапеции в прямоугольном треугольнике превращается в гипотенузу.
Получаем прямоугольный треугольник с катетом 3 см и гипотенузой 6 см. Т.е. катет равен половине гипотенузы.
А мы знаем, что катет, равный половине гипотенузы, лежит против угла в 30 градусов. Значит второй угол треугольника, который совпадает с углом равнобедренной трапеции, лежащим у нижнего основания, равен 60 градусов.
Угол при верхнем основании трапеции равен 180 — 60 = 120 градусов.
Так как сумма углов трапеции, прилежащих к боковой стороне трапеции, равна 180 градусов.
Ответ: углы трапеции равны 60, 60, 120, 120 градусов.
Успехов!
В рівнобічній трапеції менша основа дорівнює 6 см. Бічна сторона 25 см а діагональ 29 см Знайдіть площу трапеції
Добрый день, Василий!
Площадь трапеции, как известно, равна произведению полу-суммы оснований и высоты.
Опустим две высоты на нижнее основание трапеции.
Получили два равных прямоугольных треугольника и прямоугольник с длиной стороны 6 см.
Поскольку обе высоты в трапеции равны между собой, то можно составить уравнение.
Примем левую и правую части большего основания за х.
Тогда из левого треугольника можно написать, что высота равна 25 квадрат — х квадрат.
С другой стороны, эта же высота равна из треугольника в гипотенузой 29
29 квадрат — (х + 6) квадрат.
Решая это уравнение, получим х = 15.
Значит, нижнее основание равно 15 + 15 + 6 = 36.
Из левого треугольника находим высоту. Она равна корень из 25 в квадрате — 15 в квадрате.
Получим, что высота равна 20 см.
Находим площадь трапеции:
1/2 * ( 36+6) * 20 = 420 кв. см.
Успехов в учебе!