 Добрый день, друзья!
Добрый день, друзья!
Тема сегодняшнего поста: решить тригонометрическое уравнение.
Эти уравнения, объединённые в задание № 13 различны,
но их всех объединяет одно -
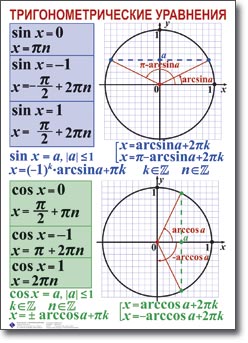
умение решать простейшие тригонометрические уравнения.
 Задача 1.
Задача 1.
а). Решите уравнение 6sin²x — 5sinx — 4 = 0
б). Найдите все корни этого уравнения, принадлежащие отрезку
[-7π/2;-3π/2].
Решение:
а). в данном случае мы имеем простейшее квадратное уравнение относительно sinx.
Пусть sinx = t≤|1| Тогда:
6t² — 5t — 4 = 0.
Дискриминант данного уравнения положительный, т.к. свободный член имеет знак минус.
D = 25 + 4•6•4 = 25 + 96 = 121 = 11².
Отсюда находим корни уравнения:
t1 = (5+11)/12 = 16/12 = 4/3. Данный корень не подходит из-за t≤|1|.
t2 = (5-11)/12 = -1/2.
sinx = -1/2.
Решаем это простейшее уравнение методом трёх шагов.
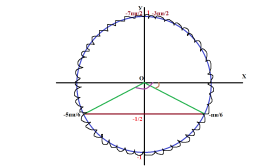
Шаг 1. Отмечаем на оси OY значение sinx = -1/2.
Шаг 2. Через эту точку проводим перпендикуляр к оси OY до пересечения с тригонометрическим кругом.
Получим две точки на круге, которые и будут нашими искомыми углами.
Шаг 3. Соединяем точки тригонометрического круга с началом координат и отмечаем углы между положительным направлением оси ОХ и радиус-вектором.
В нашем случае первый угол будет -π/6, второй угол -5π/6.
Пишем ответ на задание
а). х1 = -π/6 + 2πk, где k∈Z;
х2 = -5π/6 + 2πn, где n∈Z.
б). Отметим на тригонометрическом круге дугу от [-7π/2 до -3π/2].
Для того, чтобы это было наглядно видно, представим дугу в виде
-21π/6 до -9π/6.
В этот промежуток попадают наши искомые углы из ответа а).
Но для того, чтобы они вошли в этот промежуток, необходимо к каждому из углов добавить по отрицательному периоду, т.е. по -2π.
Тогда первый угол -π/6 войдёт в промежуток, как -π/6 — 2π = -13π/6.
А второй — 5π/6 — 2π = -17π/6.
Ответ:
а). х1 = -π/6 + 2πk, где k∈Z; х2 = -5π/6 + 2πn, где n∈Z.
б). -13π/6, -17π/6.
Задача 2.
а). Решите уравнение 7sin²x + 8cosx — 8 = 0
б). Найдите все корни этого уравнения, принадлежащие отрезку
[-π/2; π/2].
Решение:
а). Поскольку в этом уравнении косинус угла стоит в первой степени, а его синус — во второй,
то для того, чтобы перейти к квадратному уравнению относительно косинуса, необходимо воспользоваться основным тригонометрическим тождеством.
sin²x + cos²x = 1 ⇔ sin²x = 1 — cos²x
Имеем:
7(1 — cos²x) + 8cosx — 8 = 0
7 — 7cos²x + 8cosx — 8 = 0
7cos²x — 8cosx + 1 = 0
Мы вышли на квадратное уравнение относительно cosx.
В этом уравнении сумма коэффициентов при неизвестном и свободного члена равна нулю.
А это значит, что один из корней равен 1.
Второй корень находим по теореме Виета. Он равен 1/7.
cosx = 1 ⇔ x = 2πk, где k∈Z;
cosx = 1/7.
Шаг 1. Отмечаем на оси ОХ значение cosx = 1/7.
Шаг 2. Через эту точку проводим перпендикуляр к оси ОХ до пересечения с тригонометрическим кругом.
Получим две точки на круге, которые и будут нашими искомыми углами.
Шаг 3. Соединяем точки тригонометрического круга с началом координат и отмечаем углы между положительным направлением оси ОХ и радиус-вектором.
В нашем случае первый угол будет равен arccos(1/7),
второй равен -arccos(1/7).
Пишем ответ на задание
а). х1 = 2πk, где k∈Z;
х2 = arccos(1/7) + 2πn, где n∈Z;
х3 = — arccos(1/7) + 2πm, где m∈Z;
б). Отметим на тригонометрическом круге дугу от [-π/2 до π/2].
В эту дугу войдут все три корня нашего уравнения.
Ответ:
а). х1 = 2πk, где k∈Z; х2 = arccos(1/7) + 2πn, где n∈Z;
х3 = — arccos(1/7) + 2πm, где m∈Z;
б). — arccos(1/7); 0; arccos(1/7)
На сегодня всё.
Успехов и до новых задач!
Вам так же будет интересно:
 Решить уравнение тригонометрическое 2
Решить уравнение тригонометрическое 2
 Добрый день, друзья!
Добрый день, друзья!

