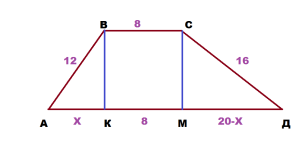
 Задача. Дана трапеция с основаниями 8 и 28 и боковыми сторонами 12 и 16.
Задача. Дана трапеция с основаниями 8 и 28 и боковыми сторонами 12 и 16.
Найти высоту трапеции.
Решение: Опустим из вершин В и С высоты
ВК и СМ на основание АД.
Получим два прямоугольных треугольника АВК и ДСМ
и прямоугольник ВСМК.
КМ в прямоугольнике равна 8, примем АК за Х,
тогда МД будет равно 28 — 8 — Х = 20 — Х.
Поскольку катеты ВК=СМ, то, решая эти треугольники по теореме Пифагора,
составим следующее уравнение:
12² — Х² = 16² — (20 — Х)²
144 — Х² = 256 -(400 — 40Х + Х²)
144 — Х² = 256 — 400 + 40Х — Х²
144 — 256 + 400 = 40Х
40Х = 288
Х = 7,2
Из треугольника АВК находим ВК.
ВК² = 12² — 7,2²
ВК² = 92,16
ВК = 9,6
Ответ: высота трапеции 9,6
Прочитать остальную часть записи »
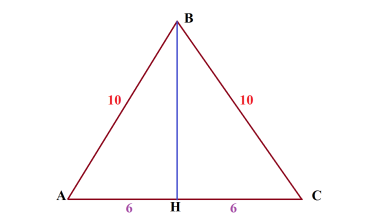 Здравствуйте, друзья!
Здравствуйте, друзья!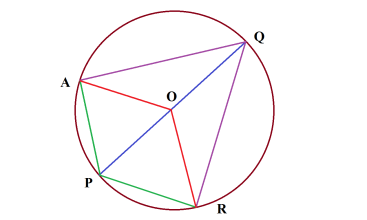 Задача. Через точку P окружности проведены диаметр PQ и две хорды
Задача. Через точку P окружности проведены диаметр PQ и две хорды Задача. Дан параллелограмм с острым углом, равным 60º. Квадраты длин диагоналей d и D параллелограмма относятся как 1:3. Необходимо найти отношение длин сторон а и b параллелограмма. Решение: Опустим из вершин В и С параллелограмма высоты на сторону АД и на её продолжение ДЕ. Получим два прямоугольных треугольника ДВК и АСЕ. Поскольку у этих треугольников равные высоты ВК и СЕ, то применим для их решения теорему Пифагора. В треугольнике АВК примем АВ за а, тогда, поскольку угол А равен 60º по условию, угол В в этом треугольнике будет равен 30º. Прочитать остальную часть записи »
Задача. Дан параллелограмм с острым углом, равным 60º. Квадраты длин диагоналей d и D параллелограмма относятся как 1:3. Необходимо найти отношение длин сторон а и b параллелограмма. Решение: Опустим из вершин В и С параллелограмма высоты на сторону АД и на её продолжение ДЕ. Получим два прямоугольных треугольника ДВК и АСЕ. Поскольку у этих треугольников равные высоты ВК и СЕ, то применим для их решения теорему Пифагора. В треугольнике АВК примем АВ за а, тогда, поскольку угол А равен 60º по условию, угол В в этом треугольнике будет равен 30º. Прочитать остальную часть записи » Задача. Дана трапеция с основаниями 8 и 28 и боковыми сторонами 12 и 16.
Задача. Дана трапеция с основаниями 8 и 28 и боковыми сторонами 12 и 16.