Геометрия — просто!

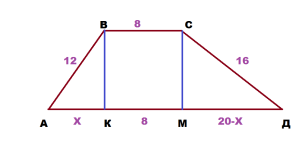
Задача. Дана трапеция с основаниями  8 и 28 и боковыми сторонами 12 и 16.
Найти высоту трапеции.
Решение: Опустим из вершин В и С высоты
ВК и СМ на основание АД.
Получим два прямоугольных треугольника АВК и ДСМ
и прямоугольник ВСМК.
КМ в прямоугольнике равна 8, примем АК за Х,
тогда МД будет равно 28 — 8 — Х = 20 — Х.
Поскольку катеты ВК=СМ, то, решая эти треугольники по теореме Пифагора,
составим следующее уравнение:
12² — Х² = 16² — (20 — Х)²
144 — Х² = 256 -(400 — 40Х + Х²)
144 — Х² = 256 — 400 + 40Х — Х²
144 — 256 + 400 = 40Х
40Х = 288
Х = 7,2
Из треугольника АВК находим ВК.
ВК² = 12² — 7,2²
ВК² = 92,16
ВК = 9,6
Ответ: высота трапеции 9,6

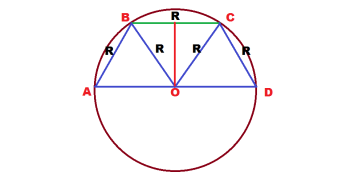Задача. Боковая сторона и меньшее основание
равнобедренной трапеции равны радиусу
описанной окружности. Найти высоту трапеции, если
её средняя линия равна 6√3.
Решение: Из условия задачи следует, что треугольники
ABO, BCO, OCD — равносторонние.

Из этого получается, что сумма углов AOB, BOC и COD равна 180º.
А раз это так, то AOD — развернутый угол,
и AD диаметр описанной окружности.
Отсюда имеем: (2R + R)/2 = 6√3.
3R/2 = 6√3
3R  = 12√3
R = 4√3.
Из равностороннего треугольника ВСО, зная сторону,
которая равна 4√3, находим высоту.
По теореме Пифагора:
Квадрат высоты = R² -(R/2)² = 16*3 — 4*3 = 48 — 12 = 36.
Отсюда, высота трапеции равна √36 = 6.
Ответ: высота трапеции равна 6.