Добрый день, друзья! Сегодня мы будем заниматься подготовкой к ОГЭ по геометрии. Для того, чтобы точно ответить на 5 вопросов модуля «Геометрия», необходимо знать основные геометрические фигуры, правила, которые с ними связаны и конечно же формулы. Так что давайте, попробуем. 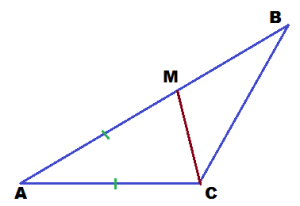 Задача 1. Дан треугольник АВС. На стороне АВ выбрана точка М таким образом, что АМ=АС. Угол А в треугольнике АВС равен 10º, а угол С этого же треугольника равен 166º. Найти угол МСВ. Решение: Нам дано, что АМ=АС. А это значит, что треугольник АМС — равнобедренный. А мы знаем, что в равнобедренном треугольнике углы при основании равны.
Задача 1. Дан треугольник АВС. На стороне АВ выбрана точка М таким образом, что АМ=АС. Угол А в треугольнике АВС равен 10º, а угол С этого же треугольника равен 166º. Найти угол МСВ. Решение: Нам дано, что АМ=АС. А это значит, что треугольник АМС — равнобедренный. А мы знаем, что в равнобедренном треугольнике углы при основании равны.
Угол при вершине треугольника АМС равен 10º. А мы знаем, что сумма внутренних углов треугольника равна 180º. Значит, на остальные 2 угла треугольника приходится 180-10 = 170º. Но углы в треугольнике АМС равны. Значит, каждый из них равен 170/2 = 85º. Угол АСМ равен 85º. Но этот угол входит в состав угла АСВ, который равен 166º. Значит, на долю другого угла, а именно МСВ приходится 166 — 85 = 81º. Ответ: угол МСВ равен 81º.
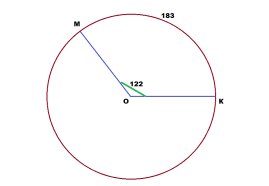 Задача 2. В окружности центральный угол МОК равен 122°. Найти длину большей дуги, если длина меньшей дуги равна 183. Решение: Длина дуги окружности зависит от величины центрального угла, который опирается на эту дугу. l=пRn/180, где l- длина дуги, n-величина центрального угла. 183 = 122пR/180 пR = 183*180/122 Большая дуга окружности измеряется центральным углом, который равен 360-122 = 238. Отсюда находим длину большей дуги: l=пRn/180 = 183*180/122 * 238/180 = 183*238/122 = 238*1.5 = 357. Ответ: Длина большей дуги равна 357.
Задача 2. В окружности центральный угол МОК равен 122°. Найти длину большей дуги, если длина меньшей дуги равна 183. Решение: Длина дуги окружности зависит от величины центрального угла, который опирается на эту дугу. l=пRn/180, где l- длина дуги, n-величина центрального угла. 183 = 122пR/180 пR = 183*180/122 Большая дуга окружности измеряется центральным углом, который равен 360-122 = 238. Отсюда находим длину большей дуги: l=пRn/180 = 183*180/122 * 238/180 = 183*238/122 = 238*1.5 = 357. Ответ: Длина большей дуги равна 357.
 Задача 3. Основания равнобедренной трапеции равны 8 и 18, а её боковые стороны равны 13. Найти площадь трапеции. Решение: Перед тем, как приступить к решению этой задачи, необходимо сделать дополнительное построение, а именно — опустить высоты из вершин В и С на основание АД. Слева и справа получим 2 прямоугольных треугольника, которые равны между собой по гипотенузе и острому углу. Значит, АМ=КД. Получается, что основание АД разбито на 3 отрезка АМ, МК и КД. МК = ВС = 8. АМ=КД = (18-8):2 = 5. Из треугольника АВМ, зная гипотенузу АВ=13, катет АМ=5, находим ВМ. ВМ = √13² — 5² = √169-25 = √144 = 12. Высота трапеции равна 12. Площадь трапеции находим по формуле: S = (8+18)/2 * 12 = 156. Ответ: Площадь трапеции 156.
Задача 3. Основания равнобедренной трапеции равны 8 и 18, а её боковые стороны равны 13. Найти площадь трапеции. Решение: Перед тем, как приступить к решению этой задачи, необходимо сделать дополнительное построение, а именно — опустить высоты из вершин В и С на основание АД. Слева и справа получим 2 прямоугольных треугольника, которые равны между собой по гипотенузе и острому углу. Значит, АМ=КД. Получается, что основание АД разбито на 3 отрезка АМ, МК и КД. МК = ВС = 8. АМ=КД = (18-8):2 = 5. Из треугольника АВМ, зная гипотенузу АВ=13, катет АМ=5, находим ВМ. ВМ = √13² — 5² = √169-25 = √144 = 12. Высота трапеции равна 12. Площадь трапеции находим по формуле: S = (8+18)/2 * 12 = 156. Ответ: Площадь трапеции 156.
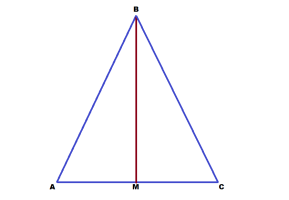 Задача 4. В треугольнике АВС АВ=ВС=35, АС=42. Найти длину медианы ВМ. Решение: поскольку в треугольнике 2 стороны равны, это треугольник — равнобедренный. А в равнобедренном треугольнике медиана угла при вершине является одновременно биссектрисой и высотой. Получается, что треугольник АВМ — прямоугольный. АВ=35, АМ=1/2 АС = 21. По теореме Пифагора находим длину медианы. ВМ² = √35² — 21² = √(35-21)(35+21) = √14*56 = √14*14*4 = 14*2 = 28. Ответ: Длина медианы равна 28.
Задача 4. В треугольнике АВС АВ=ВС=35, АС=42. Найти длину медианы ВМ. Решение: поскольку в треугольнике 2 стороны равны, это треугольник — равнобедренный. А в равнобедренном треугольнике медиана угла при вершине является одновременно биссектрисой и высотой. Получается, что треугольник АВМ — прямоугольный. АВ=35, АМ=1/2 АС = 21. По теореме Пифагора находим длину медианы. ВМ² = √35² — 21² = √(35-21)(35+21) = √14*56 = √14*14*4 = 14*2 = 28. Ответ: Длина медианы равна 28.
 Задача 5. В трапеции АВСД основания равны 4 и 1, а её площадь равна 35. Найти площадь треугольника АВС. Решение: площадь трапеции равна произведению полу-суммы оснований на высоту. Отсюда, высота трапеции равна 35:2,5 = 14. Площадь треугольника АВС равна половине произведения основания на высоту. Основание треугольника равно 1, высота 14. Площадь равна 7. Ответ: площадь треугольника равна 7.
Задача 5. В трапеции АВСД основания равны 4 и 1, а её площадь равна 35. Найти площадь треугольника АВС. Решение: площадь трапеции равна произведению полу-суммы оснований на высоту. Отсюда, высота трапеции равна 35:2,5 = 14. Площадь треугольника АВС равна половине произведения основания на высоту. Основание треугольника равно 1, высота 14. Площадь равна 7. Ответ: площадь треугольника равна 7.
На сегодня всё. Успехов и до новых задач! В субботу 28 марта девятиклассники пишут пробный ОГЭ по математике. Ни пуха, ни пера!
Вам так же будет интересно:
 Подготовка к ОГЭ по геометрии
Подготовка к ОГЭ по геометрии
 Задача 1. Дан треугольник АВС. На стороне АВ выбрана точка М таким образом, что АМ=АС. Угол А в треугольнике АВС равен 10º, а угол С этого же треугольника равен 166º. Найти угол МСВ. Решение: Нам дано, что АМ=АС. А это значит, что треугольник АМС — равнобедренный. А мы знаем, что в равнобедренном треугольнике углы при основании равны.
Задача 1. Дан треугольник АВС. На стороне АВ выбрана точка М таким образом, что АМ=АС. Угол А в треугольнике АВС равен 10º, а угол С этого же треугольника равен 166º. Найти угол МСВ. Решение: Нам дано, что АМ=АС. А это значит, что треугольник АМС — равнобедренный. А мы знаем, что в равнобедренном треугольнике углы при основании равны.





