Геометрия — просто!

Добрый день!
Сегодня без предисловий начнём сразу решать задачи для подготовки к ОГЭ по геометрии биссектрисы угла и не только.
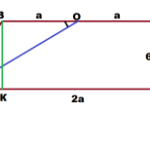
Задача 1. Дана трапеция АВСД, Биссектрисы её углов А и В пересекаются точке М, а биссектрисы углов С и Д — в точке К.
Найти МК, если АД равно 20, ВС равно 10, АВ равно 13, СД равно 15.
Решение: Как мы определили в прошлой задаче треугольники АВМ и ДКС — прямоугольные.
Вместе с тем, FG — средняя линия трапеции. Действительно, средняя линия параллельна основаниям и поэтому углы МАД и FМА равны как накрест лежащие.
Но АМ — биссектриса угла А, значит, угол FМА равен углу МАВ, т.е. треугольник AFM — равнобедренный. И поэтому, AF = FM.
Но тогда и BF=FM. И получается, что FM делит сторону АВ пополам. Отсюда FM = АВ/2 = 13/2 = 6,5
Точно так же  получаем, что KG = 15/2 = 7,5.
Из условия задачи имеем, что средняя линия FG равна (20+10):2 = 15.
Отсюда, МК = 15 — 6,5 — 7,5 = 1
Ответ: МК=1.

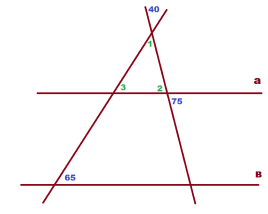Задача 2.  По данным рисунка докажите, что прямые а и b параллельны.
Решение: Рассмотрим угол 1 и угол в 40°. Эти углы вертикальные, а вертикальные углы равны.
Значит, угол 1 = 40°.
Угол 2 и угол в 75° тоже вертикальные.
Значит, угол 2 равен 75°.
Сумма внутренних углов треугольника, как мы знаем, равна 180°.
Имея 2 угла, можно найти третий: угол 3 = 180 — угол 1 — угол 2, или  180 — 40 — 75 = 65°.
     Но углы 3 и 65° — соответственные при прямых а и b и секущей 1-65.
Угол 3=65°, как мы только что выяснили. А мы знаем, что если при пересечении двух прямых третьей окажется, что какие -то соответственные углы равны, то эти прямые параллельны.
Вот и получается, что прямые а и b параллельны.

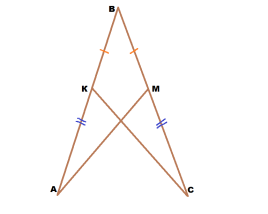Задача 3. На рисунке АК=СМ, ВК=ВМ. Доказать, что АМ=СК.
Решение: Рассмотрим 2 треугольника: АВМ и СВК.
В этих треугольниках АВ = ВС, т.к. если к равному прибавить равное, то получится равное.
К равным величинам АК и СМ прибавили равные величины КВ и ВМ.
ВМ=ВК по условию.
Угол В — общий.
Треугольники равны по первому признаку равенства треугольников (по двум сторонам и углу, заключённому между ними).
А в равных треугольниках против равных углов лежат равные стороны. В треугольнике АВМ против угла В лежит сторона АМ, а в треугольнике СВК против угла В лежит сторона СК.
Значит  АМ=СК.

Задача 4. В треугольнике АВС проведены биссектрисы АО и СО. Угол АОС равен 100°. Найти внешний угол при вершине В.
Решение: Рассмотрим треугольник АОВ. Сумма внутренних углов в нём равна 180°.
Т.е  α + β + 100 = 180,
или   α + β = 180 — 100 = 80.
Рассмотрим треугольник АВС. В нём  сумма внутренних углов тоже равна 180°.
А именно 2α + 2β + В = 180.
Но, α + β = 80, значит,
2α + 2β = 80*2 = 160. Получается, что сумма углов А и С треугольника АВС равна 160°.
А мы знаем, что внешний угол треугольника равен сумме внутренних, не смежных с ним. Получается, что внешний угол при вершине В равен 160°.
Ответ: внешний угол при вершине В равен 160°.

На сегодня всё. В следующий раз мы продолжим решать геометрические задачи для подготовки к ОГЭ.