Геометрия — просто!

Здравствуйте,  уважаемые читатели! Сегодня мы  приступим к решению  задач по свойствам биссектрисы и медианы треугольника. А для начала  давайте вспомним, что такое биссектриса и медиана.
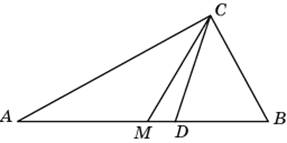
       Биссектриса — это отрезок CD, который выходит из вершины угла треугольника, делит угол пополам и заканчивается на противоположной стороне.
       Медиана – это отрезок СМ, который соединяет вершину треугольника с серединой противоположной стороны.
Поскольку в треугольнике вершин и сторон по три, то биссектрис медиан у него будет тоже три.

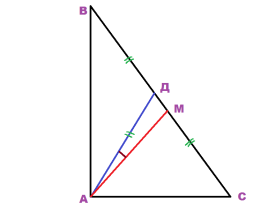Задача 1. Дан прямоугольный треугольник АВС. Из вершины А  к стороне ВС проведены медиана АД и биссектриса АМ. Угол между медианой и биссектрисой равен 17°. Найти острые углы треугольника.
Решение: Поскольку АМ — биссектриса, то угол ВАМ равен углу МАС и они равны 45°. Но угол ДАМ равен 17°. Отсюда, угол ВАД равен разности углов ВАМ и ДАМ, или 45-17 = 28°.
         Мы знаем, что медиана, проведённая из вершины прямого угла прямоугольного треугольника, делит этот треугольник на 2 равнобедренных треугольника. А именно треугольники АВД и АДС.
         И теперь, поскольку треугольник АВД равнобедренный, то углы при основании у него равны, т.е. угол ВАД равен углу АВД и они оба равны 28°.
А это значит, что в прямоугольном треугольнике угол В равен 28°.
         Но сумма острых углов в прямоугольном треугольнике равна 90°. Отсюда, угол С будет равен 90 — 28 = 62°.
Ответ: острые углы в прямоугольном треугольнике равны 28° и 62°.

Задача 2. Докажите, что биссектрисы смежных углов перпендикулярны.
Решение: Мы знаем свойство измерения углов, которое гласит, что если внутри угла провести лучи, то они разобьют его на несколько углов и сумма градусных мер этих углов будет равна градусной мере первоначального угла.
Поэтому мы имеем: α+α+β+β = 180°.
Или 2α+2β = 180°.
         Сокращаем правую и левую часть уравнения на 2, получим:   α + β = 90°.
          Т.е. угол ДВК между биссектрисами  ВД и ВК смежных углов ВСЕГДА равен 90° независимо от величин смежных углов.

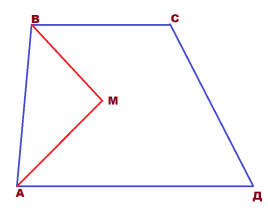Задача 3. Дана трапеция АВСД. Биссектрисы углов А и В пересекаются в точке М.
Найти АВ, если АМ = 24, ВМ = 18.
Решение: Из предыдущей задачи мы узнали, что биссектрисы смежных углов всегда образуют угол 90°.
Биссектрисы, проведённые из углов трапеции, прилежащих к боковой стороне тоже образуют угол 90°.
     В самом деле: углы А и В трапеции в сумме дают 180°, как односторонние углы при параллельных прямых АД и ВС и секущей АВ.
      Значит, половины этих углов в сумме будут равны 90°.
А если в треугольнике 2 угла в сумме равны 90°, то третий угол будет равен 90°, ведь сумма внутренних углов треугольника равна 180°.
Значит, это треугольник — прямоугольный. Нам известно в нём 2 катета, найти гипотенузу можно по теореме Пифагора.
АВ² = АМ² + ВМ² = 24² + 18² = 900. Отсюда, АВ = 30.
Ответ: АВ = 30.

На сегодня мы заканчиваем решать задачи по свойствам биссектрисы и медианы треугольника. В следующий раз мы продолжим решать геометрические задачи.