Геометрия — просто!

Добрый день, друзья! Сегодня из «Сборника задач для поступающих во ВТУЗы» мы будем решать задачи по геометрии прямоугольного треугольника.
Такие треугольники примечательны тем, что у них присутствуют некоторые особенности,  которых нет у простых треугольников, а именно.
Катет прямоугольного треугольника, лежащий против угла в 30º равен половине гипотенузы.
Это правило вообще-то необходимо запомнить накрепко, особенно тем ученикам, которые собираются в 10-11 классы.
Поскольку с помощью него  будут рассчитаны  многие значения углов в тригонометрии.
Ещё правило — медиана прямоугольного треугольника, проведённая  из вершины прямого угла, равна половине гипотенузы.
Т.е. она образует два равнобедренных треугольника.
Пока на этом остановимся и перейдём к задачам.

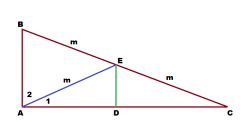Задача 1. Медиана гипотенузы прямоугольного треугольника равна m и делит прямой угол в отношении 1:2. Найти стороны треугольника.
Решение: Поскольку медиана делит прямой угол в отношении 2:1, то принимая  1 за Х, а 2 за 2Х получим 3Х=90, или Х=30.
Медиана разделила прямой угол на 2 угла: 60º и 30º.
 Так как ВЕ=ЕС=m, то треугольник АВЕ — равнобедренный с углом при основании 60º.
Но если один угол при основании  равнобедренного треугольника равен 60º, то и другой тоже будет 60º.
А так как сумма внутренних углов треугольника равна 180º, то на третий угол приходится 180-60-60=60º.
Т.е. треугольник АВЕ — равносторонний, а это значит, что АВ=m.
Нам осталось найти второй катет АС.
Из треугольника АЕС мы видим, что АЕ=ЕС=m.
Треугольник равнобедренный, а это значит, что угол при вершине С равен 30º.
Теперь рассмотрим треугольник EDC.
ED — перпендикуляр, а также медиана угла при вершине равнобедренного треугольника АЕС.
ED = m/2, как катет, лежащий против угла в 30º.
По теореме Пифагора из треугольника EDC находим DC.
DC² = m² — (m/2)² = 3m²/4.
Или DC = m√3/2.  А вся сторона треугольника АС = m√3.
Ответ: Стороны треугольника равны АВ = m, ВС = 2m, АС =m√3.

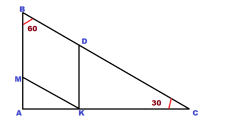Задача 2. В прямоугольный треугольник с углом 60º вписан ромб со стороной, равной 6 см так, что угол 60° у них общий и все вершины ромба лежат на сторонах треугольника.
Найти стороны треугольника.
Решение: Нам дано, что в прямоугольном треугольнике один угол равен 60°. Значит, второй угол равен 30°.
Ведь сумма острых углов в прямоугольном треугольнике равна 90°.
Так как BDKM ромб, то его противоположные стороны параллельны.
BM параллельна DK. А это значит, что при пересечении двух параллельных секущей ВС, образуются соответственные углы MBD и KDC.
Так как прямые параллельны, то углы равны по 60°.
Получилось, что в треугольнике DKC два угла равны соответственно 60° и 30°.
А это значит, что третий угол равен 90°.
Т.е. треугольник DKC прямоугольный.
Поскольку в ромбе все стороны равны, то BD=BM,  равно 6 см.
Сторона DK в треугольнике DKC тоже равна 6 см.
Но она лежит против угла в 30°.
Значит, гипотенуза DC треугольника равна  12 см.
А вся гипотенуза треугольника АВС равна 6+12 = 18 см.
Из прямоугольного треугольника АМК, в котором острые углы так же равны 30° и 60°находим катет АМ.
Он равен половине гипотенузы МК или 6:2 = 3 см.
А всего катет АВ треугольника АВС равен 6+3 = 9 см.
Остаётся найти второй катет  треугольника АВС.
Его мы находим по теореме Пифагора.
АС² = ВС² — АВ² = 18² — 9² = 324 — 81 = 243.  Отсюда, АС = √243 = 9√3.
Ответ: Стороны треугольника равны 9 см, 9√3 см и 18 см.

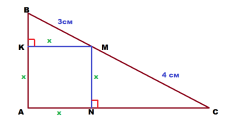Задача 3. Точка на гипотенузе, равноудалённая от обоих катетов, делит гипотенузу на отрезки длиной 3 и 4 см.
Найти катеты треугольника.
Решение: Так как как точка М равноудалена от катетов, а кратчайшее расстояние между точкой и прямой есть перпендикуляр,
то углы К и М — прямые.
Образовались прямоугольные треугольники ВКМ и MNC.
Эти треугольники подобны друг другу и треугольнику АВС.
Из подобия треугольников мы можем составить пропорцию:
МС так относится к  Х, как ВМ относится к ВК. Или 4/Х = 3/ВК.
Отсюда, ВК = 3Х/4.
Составляем другую пропорцию:
4/NC = 3/X, отсюда NC = 4Х/3.
Получается, что катет АВ равен Х + 3Х/4= 7Х/4,
а катет АС равен Х + 4Х/3 = 7Х/3.
По теореме Пифагора имеем:
(7Х/4)² + (7Х/3)² = 7²
49х²/16 + 49х²/9 = 49, или
Х²(1/16 + 1/9) = 1
25Х² = 16*9
Х = 4*3/5 = 12/5 = 2,4 см
АС = 2,4 + 2,4 * 4/3 = 2,4 + 3,2 = 5,6 см.
АВ = 2,4 + 2,4 * 3/4 = 2,4 + 1,8 = 4,2 см.
Ответ: 5,6 см; 4,2 см.

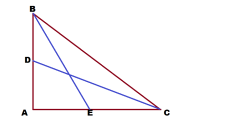Задача 4. В прямоугольном треугольнике медианы катетов равны BE = √52 и CD =√73.
Найти гипотенузу треугольника.
Решение: Примем АЕ = АС = m.
BD = AD = k.
Из прямоугольного треугольника АВЕ имеем:
(2k)² + m² = (√52)²
Из прямоугольного треугольника ADC  имеем:
k² + (2m)² = (√73)².
Решаем совместно систему двух уравнений с двумя неизвестными:
4k² + m² = 52
k² + 4m² = 73
Домножаем второе уравнение на 4 и вычитаем из первого уравнения второе:
4k² + m² -4k² — 16m² = 52 — 292
-15m² = — 240
m² = 16
m=4 см   k² + 4*4² = 73   k² = 9  k = 3 см.
Катеты треугольника АВС равны 6 см и 8 см,
По теореме Пифагора гипотенуза равна 10 см.
Ответ: гипотенуза ВС = 10 см.

На сегодня всё. В следующий раз мы продолжим решение геометрических задач для подготовки к ОГЭ.