 Добрый день, дорогие друзья!
Добрый день, дорогие друзья!
Сегодня мы продолжим тему геометрия трапеция задачи 8 класс.
И я подобрал на сегодня несколько необычные задачи.
Чем же они необычны?
Дело в том, что они из самого первого сборника под редакцией М.И. Сканави «Сборник задач по математике для конкурсных экзаменов во ВТУЗы».
Этот сборник вышел в далёком 1969 году, а задачи, которые в нём напечатаны, я даю своим ученикам, начиная с 8 класса.
ВТУЗ — это высшее техническое учебное заведение (институт), которое готовило инженеров, т.е. людей с математическим складом ума. Итак: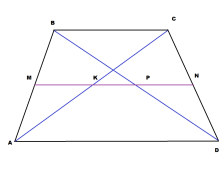
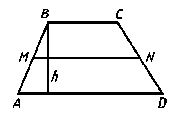
Задача 1. Большее основание трапеции равно 24 см. Найдите её меньшее основание, если расстояние между серединами её диагоналей равно 4 см.
Решение: По условию задачи AD=24 см, KP=4 см.
Если KP — расстояние между серединами диагоналей, то КР лежит на средней линии MN трапеции.
А это значит, что средняя линия трапеции включает в себя среднюю линию MP треугольника ABD.
А мы знаем, что средняя линия треугольника параллельна основанию и равна его половине.
Т.е. MP равно половине от 24 см, или 12 см.
Итого имеем MK+KP = 12 см или MK+4=12 см. Отсюда MK = 12-4 = 8 см.
Но МК является средней линией для треугольника АВС, параллельно основанию ВС и равна его половине.
Поскольку средняя линия равна 8 см, то основание будет в 2 раза больше, или 16 см.
Ответ: Меньшее основание трапеции ВС равно 16 см.
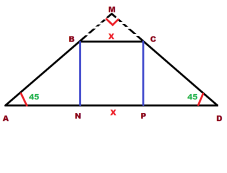 Задача 2. Боковые стороны равнобедренной трапеции при их продолжении пересекаются под прямым углом. Найти все стороны трапеции, если её площадь равна 12 см², а высота равна 2 см.
Задача 2. Боковые стороны равнобедренной трапеции при их продолжении пересекаются под прямым углом. Найти все стороны трапеции, если её площадь равна 12 см², а высота равна 2 см.
Решение: Поскольку угол М равен 90º, а трапеция равнобедренная, то и треугольник AMD будет равнобедренный и прямоугольный.
А мы знаем, что острые углы в таком треугольнике равны 45°.
Поскольку BN и СР — высоты трапеции, они образуют прямые углы.
Значит, треугольники ABN и DCP — прямоугольные.
Но у них есть по одному острому углу, равному 45°.
А мы знаем, что сумма острых углов в прямоугольном треугольнике равна 90°, следовательно, углы в этих треугольниках при вершинах В и С будут так же по 45°.
А это значит, что данные треугольники будут также прямоугольные и равнобедренные.
Отсюда BN=AN=2 см, CP=DP=2 см. И мы можем составить уравнение для площади трапеции.
Площадь трапеции равна произведению полу-суммы оснований на высоту.
(2+х+2+х) / 2 * 2 = 12 2х+4 = 12 2х = 8 х = 4см.
Верхнее основание ВС = 4 см.
Нижнее основание AD= 2+4+2 = 8 см.
Боковые стороны AB и CD находим из прямоугольных треугольников по теореме Пифагора.
Оба катета в треугольниках равны по 2 см, значит, гипотенуза в них будет 2√2 см.
Ответ: 4 см, 8 см, 2√2 см, 2√2 см.
 Задача 3. Один из углов трапеции равен 30°, а боковые стороны при продолжении пересекаются под прямым углом. Найти меньшую сторону трапеции, если её средняя линия равна 10 см, а одно из оснований равно 8 см.
Задача 3. Один из углов трапеции равен 30°, а боковые стороны при продолжении пересекаются под прямым углом. Найти меньшую сторону трапеции, если её средняя линия равна 10 см, а одно из оснований равно 8 см.
Решение: В трапеции ABCD средняя линия равна 10 см.
Значит, по определению средней линии трапеции получаем сумму оснований трапеции, равной 10*2 = 20см.
Одно из оснований равно 8 см, значит, второе основание будет 20-8 = 12 см.
Получается, что AD=12 см, ВС=8 см.
Из треугольника AKD, где К — прямой угол, имеем: АК лежит против угла в 30°, значит АК равно половине гипотенузы треугольника, или половине AD. т.е. 12:2 = 6 см.
Теперь рассмотрим треугольник ВКС.
Этот треугольник подобен треугольнику AKD, поскольку они оба прямоугольные, а углы ВСК и ADK равны, как соответственные при параллельных прямых ВС и AD и секущей CD.
Значит, угол ВСК тоже равен 30°.
Отсюда имеем, что ВК равно половине ВС, или 8:2 = 4 см.
Тогда АВ = АК — ВК = 6 — 4 = 2 см.
А точно ли она меньшая?
Из двух прямоугольных треугольников АВМ и CND ВМ=CN. Угол D=30°, угол А=60°.
АВ=ВМ:sin 60° ≈1.15 ВМ, а CD = ВМ:sin30° = 2ВМ.
Получается, АВ меньшая сторона.
Ответ: Меньшая боковая сторона трапеции равна 2 см.
 Задача 4. Длины параллельных сторон трапеции AD и BC равны соответственно 25 см и 4 см, а длины непараллельных сторон АВ и CD — 13 см и 20 см. Найти площадь трапеции.
Задача 4. Длины параллельных сторон трапеции AD и BC равны соответственно 25 см и 4 см, а длины непараллельных сторон АВ и CD — 13 см и 20 см. Найти площадь трапеции.
Решение: площадь трапеции равна произведению полу-суммы оснований на высоту.
Основания нам известны, значит, осталось найти высоту.
Сделаем дополнительные построения — проведём высоты трапеции ВМ и CN из точек В и С.
И рассмотрим два прямоугольных треугольника АВМ и CND.
По теореме Пифагора выразим в каждом из них квадрат высоты трапеции и приравняем друг к другу.
Примем АМ за Х, тогда MN будет равно 4, а ND = 21-Х.
Из первого треугольника имеем ВМ² = 13² — Х².
Из второго треугольника имеем CN² = 20² — (21 — Х)².
Поскольку ВМ=CN, приравняем два выражения.
13² — Х² = 20² — (21 — Х)²
169 — Х² = 400 — 441 + 42Х — Х²
42Х = 169 — 400 + 441
42Х = 210 Х = 5
Из треугольника АВМ при гипотенузе 13 см и катете 5 см находим второй катет:
ВМ = √13² — 5² = √169 — 25 = √144 = 12.
Высота трапеции равна 12 см.
Отсюда, площадь трапеции считаем: (25+4)/2 * 12 = 174см².
Ответ: площадь трапеции равна 174 см².
На сегодня всё. В следующий раз мы продолжим решение задач на тему геометрия трапеция 8 класс.
Успехов!
Вам так же будет интересно:
 Геометрия трапеция задачи 8 класс.
Геометрия трапеция задачи 8 класс.
 Добрый день, дорогие друзья!
Добрый день, дорогие друзья!
 Задача 2. Боковые стороны равнобедренной трапеции при их продолжении пересекаются под прямым углом. Найти все стороны трапеции, если её площадь равна 12 см², а высота равна 2 см.
Задача 2. Боковые стороны равнобедренной трапеции при их продолжении пересекаются под прямым углом. Найти все стороны трапеции, если её площадь равна 12 см², а высота равна 2 см. Задача 3. Один из углов трапеции равен 30°, а боковые стороны при продолжении пересекаются под прямым углом. Найти меньшую сторону трапеции, если её средняя линия равна 10 см, а одно из оснований равно 8 см.
Задача 3. Один из углов трапеции равен 30°, а боковые стороны при продолжении пересекаются под прямым углом. Найти меньшую сторону трапеции, если её средняя линия равна 10 см, а одно из оснований равно 8 см. Задача 4. Длины параллельных сторон трапеции AD и BC равны соответственно 25 см и 4 см, а длины непараллельных сторон АВ и CD — 13 см и 20 см. Найти площадь трапеции.
Задача 4. Длины параллельных сторон трапеции AD и BC равны соответственно 25 см и 4 см, а длины непараллельных сторон АВ и CD — 13 см и 20 см. Найти площадь трапеции.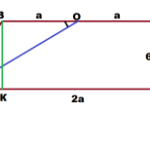


И кто же интересно Вам сказал, что в задаче 4 основания высот попадают на основание трапеции? Такое решение на «двоечку» тянет)
Андрей, добрый вечер!
Я не понимаю Вашего сарказма, но во всех остальных случаях получается, что катет ND прямоугольного треугольника CND, будет больше гипотенузы CD.
Проверьте на чертежах.
С уважением
Сергей