Геометрия — просто!

Добрый день, дорогие друзья!
Сегодня мы продолжим решение задач из сборника под редакцией М.И. Сканави.
И на этот раз мы будем решать задачи по геометрии   параллелограмма.
Понятно, что прежде, чем приступать к решению таких задач, надо понимать, что такое параллелограмм и какие у него есть свойства.
Параллелограмм — выпуклый четырёхугольник, у которого противоположные стороны попарно параллельны.
У параллелограмма противоположные стороны и противоположные углы равны;
диагонали его делят параллелограмм на 2 равных треугольника,
а сами диагонали точкой пересечения делятся пополам.
И сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Вот в основном те свойства, которые в первую очередь необходимы для понимания и решения задач по геометрии параллелограмма. А теперь задачи.
Задача 1. Периметр параллелограмма равен 90 см, а его острый угол равен 60°.
Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма.
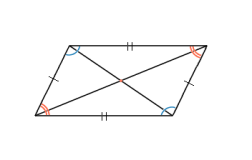
Решение: Если угол А равен 60°, то угол В, лежащий рядом с ним , будет равен 180-60=120°.
Но диагональ BD делит его в соотношении 1:3, или на 4 равные части.
Получается, что одной части принадлежит 120:4 = 30°.
Следовательно, диагональ BD делит угол В на 2 угла 30° и 90°.
По рисунку угол 1 — прямой. Треугольник ABD — прямоугольный.
И угол 2 в треугольнике равен 30º, как накрест лежащий при параллельных прямых AB и CD и секущей BD.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, что АВ=1/2 AD.
Теперь составляем уравнение для периметра.
AB+BC+CD+AD=90
1/2AD+AD+1/2AD+AD= 90
3AD=90  AD=30    AB=1/2*30 = 15.
Ответ: стороны параллелограмма равны 30 см и 15 см.

Задача 2. Биссектриса острого угла параллелограмма делит его диагональ на отрезки длиной 3,2 см и 8,8 см.
Найти стороны параллелограмма, если его периметр равен 30 см.
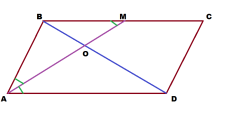
Решение: Мы знаем, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные  сторонам угла.
А именно, AB:AD = BO:OD, но BO и OD равны соответственно 3,2 см и 8,8 см.
Поэтому, можно принять, что АВ = 3,2х, а AD равно 8,8х.
Противоположные стороны параллелограмма равны.
Периметр это есть сумма всех сторон параллелограмма.
Составляем уравнение:  3,2х+8,8х+3,2х+8,8х = 30  24х = 30   х = 30/24 = 5/4.
Мы нашли коэффициент пропорциональности Х=5/4.
Отсюда, сторона АВ = 3,2х = 3,2 * 5/4 = 4 см.
Сторона AD равна 8,8х = 8,8 * 5/4 = 11 см.
Ответ: стороны параллелограмма равны 4 см, 4 см, 11 см, 11 см.

Задача 3. Параллелограмм с периметром 44 см разделён диагоналями на 4 треугольника.
Разность между периметрами двух смежных треугольников равна 6 см.
Найти стороны параллелограмма.
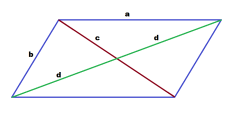
Решение: Рассмотрим два треугольника, лежащих выше диагонали d.
Периметр первого равен b+c+d.
Периметр второго равен a+c+d.
Разность периметров двух треугольников равна 6 см.
Составляем уравнение:
a+c+d — (b+c+d) = a+c+d-b-c-d = a-b = 6.
Получилось, что разность двух сторон параллелограмма равна 6 см.
Второе уравнение составляем из свойства периметра параллелограмма:
a+b+a+b = 44
2a+2b=44
a+b=22.
Получили систему двух уравнений с двумя неизвестными:
a — b = 6
a + b = 22             Решим её методом сложения. Сложим левые и правые части уравнений. Получим:
a — b + a + b = 6 + 22     2a = 28    a = 14.
a — b = 6   b = a — 6 = 14 — 6 = 8.
Ответ: Стороны параллелограмма равны 14 см, 14 см, 8 см, 8 см.

Задача 4. Перпендикуляр, опущенный из вершины параллелограмма на его диагональ, делит эту диагональ на отрезки АМ и МС длиной 6 см и 15 см соответственно.
Разность сторон параллелограмма равна 7 см.
Найти длины сторон и диагонали параллелограмма.
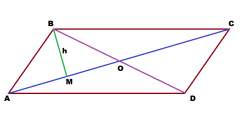
Решение: Примем сторону AB за  a, сторону  BC за  b.
Из двух прямоугольных треугольников АВМ и ВМС выразим равный для них катет ВМ по теореме Пифагора.
АВ² — АМ² = ВС² — МС².
Подставляем вместо сторон известные выражения:
а² — 6² = b² — 15²  или   15² — 6² = b² — а²   (b — а) (b + а) = (15 — 6) (15 + 6),
но b — а = 7
7 (b + а) = 9 * 21   b + a = 9 * 3 = 27.
Имеем систему двух уравнений с двумя неизвестными, как в задаче 3.
b + a =  27
b — а = 7                Отсюда получаем 2b = 34   b = 17,  a = 27 — 17 = 10.
Теперь, зная стороны параллелограмма, мы можем найти высоту ВМ.
ВМ² = 10² — 6² = 64. Отсюда ВМ = 8 см.
А теперь, из прямоугольного треугольника ВМО находим ВО.
ВМ = 8 см,
МО = АО — АМ = АС/2 — АМ = (6+15)/2 — 6 = 21/2 — 6 = 10,5 — 6 = 4,5 см.
По теореме Пифагора находим ВО.
ВО² = 8² + 4,5² = 64 + (9/2)² = 64 + 81/4 = 337/4. Или ВО = √337/2.
Поскольку BD в 2 раза больше, чем ВО, то её длина будет равна √337.
Ответ: Длины сторон параллелограмма 17 см, 17 см, 10 см, 10 см. Длина диагонали √337.

На сегодня всё. В следующий раз мы продолжим решение задач по геометрии  из «Сборника  для поступающих во ВТУЗы». Успехов!

Комментарии (4) на “Задачи по геометрии параллелограмм.”